Forecasting the weather

The objective of this work was to predict the month of January 2023 based on data collected from 1991 to 2022, including hourly, daily and monthly records of Eixample (Barcelona). Our intention was to obtain data and later compare it with the real events that occurred in January 2023, to determine the accuracy of the algorithm in its approximation to reality.

How have we done it?

• First, we obtained the air quality data for Catalonia from the corresponding database, specifically focusing on the city of Eixample. These data covered from 1991 to 2022. We carried out an exhaustive analysis of this data to study its behavior over the years and understand its evolution, here is how it went. After carefully analyzing the collected information, we set ourselves the challenge of predicting the future based on this historical data. We use appropriate techniques and models to carry out these predictions, taking into account the patterns and trends observed in previous years.

How did we start?

• Initially, we already had the necessary historical data. Using RStudio and the Prophet library, which allows making predictions based on past data, we made a forecast that generated a table with the predicted values. In this case, we focused only on the "yhat" value of that table, which represented the prediction for the future. Subsequently, we collected the actual data corresponding to the month of January 2023. With these data in hand, we were able to establish a relationship between the generated predictions and the actual values.

How have we worked with Prophet?

• To carry out this process using RStudio, we first had to install the Prophet library, since without it we would not be able to execute the necessary functions. Next, we created a table using the CSV file obtained from the Catalonia database.
• Before running the Prophet function, we had to make some changes to the data. First, we rename the columns using the colnames function. Also, we had to change the class of the date column (originally "date") to POSIXct to make sure the data was in the correct format.
• Next, we build a model using the existing data and set a 31-day period. This allowed us to predict the data for the month of January 2023, based on the historical data provided up to the last day of 2022. Finally, we used the plot function in the model, specifying "forecast", which generated a table with the predicted values for the month of January 2023.

How do I know if the prediction made is correct?

• To verify the accuracy of the prediction, we downloaded the Eixample database again, but this time we only focused on the month of January 2023. We imported this new CSV file as a table in RStudio. Next, we select only the column corresponding to the pollutant that we have predicted, eliminating the other columns.
• In the resulting table, we make sure that both the date and the actual pollutant values are ordered in the same format (Year-Month-Day Hour:Minute:Second), as we need them to match in order to relate them correctly. We then use the merge function to combine the date, the predicted values, and the actual values into a single table.
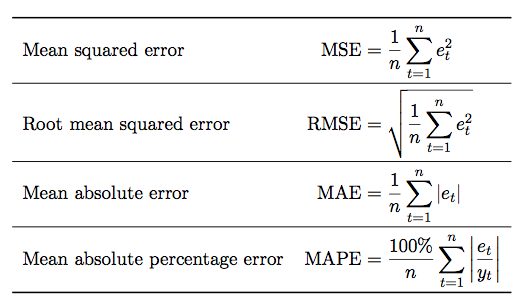
• In this project, we have conducted an analysis of PM10 data. Using the Prophet model, we obtained predictions for the data and compared them with the actual data to determine if there were significant differences. To assess the accuracy of our predictions, we employed several metrics: Mean Error (ME), Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), Mean Percentage Error (MPE), Mean Absolute Percentage Error (MAPE), and Mean Absolute Scaled Error (MASE).

These metrics serve different purposes in evaluating predictions. Here's a brief explanation of each:

• Mean Error (ME) provides a measure of the average deviation between predictions and actual values. A ME value close to zero indicates good agreement between predictions and actual data.
• Root Mean Squared Error (RMSE) measures the dispersion of prediction errors. It is particularly useful for identifying outliers or large errors as it penalizes larger errors more heavily.
• Mean Absolute Error (MAE) calculates the average magnitude of errors without considering their direction. It is a robust measure that is not influenced by outliers.
• Mean Percentage Error (MPE) provides a measure of the relative accuracy of predictions compared to actual values. It indicates the tendency to underestimate or overestimate values.
• Mean Absolute Percentage Error (MAPE) is similar to MPE but calculates the relative error as an absolute percentage, allowing for comparison of accuracy across different datasets.
• Mean Absolute Scaled Error (MASE) compares prediction errors to a reference model. It enables evaluation of the predictive capability of the model relative to a naive or standard approach.

These metrics provide an objective evaluation of the quality of our predictions and help us understand the accuracy and error trends in our prediction model. For all these metrics, a lower value indicates a better prediction, as it suggests smaller errors or a closer match between the predicted and actual values. To use this command and do it all in one, with the library forecast, I have used the command accuracy() and I got all of this values. These are the resoults that I got.

A probem I have had

One of the most significant problems I have faced recently is the lack of updating the version of RStudio on the computer I was working with. This limitation prevented me from continuing with my tasks because, when trying to execute the action of the "prophet" package, it indicated that the appropriate version of "rstan" could not be found. Due to this issue, I couldn't make progress in my work until I decided to use another computer with a newer version of RStudio. From that moment on, I was able to work smoothly.

I have also had a precision problem in my work where I was using inaccurate data comparisons. I was using the r^2 ( doing an lm) and t-student tests, but after conducting some research in this field, I realized that I needed to change my data comparison metrics. That's why we have ended up using ME, RMSE, MAE, MPE, and MAPE, as all of these metrics are more precise in comparing the data.

Another way to predict the future

• To enhance our ability to predict the future more accurately, it is crucial to explore different paths and approaches. In our case, in order to determine which algorithm is more effective in predicting the future, we initially employed the Prophet model. However, we have also decided to experiment with the auto.arima model from the forecast library. By doing so, we aim to obtain prediction values and subsequently compare them with the actual data, ultimately determining which algorithm aligns more closely with reality.

What steps do we have to follow?

• The first step is to download the forecast library. Once we have the library, we need to gather the historical data that we have already analyzed. Then, we can proceed with using the auto.arima function. After applying several steps, I specifically instructed the function to generate predictions for the month of January 2023. Upon requesting the print output, I obtained a set of values. However, they were not ordered by dates when displayed in the console, which made them less useful to me. To address this, I saved the values as a CSV file and then read the file using the read.csv function. This allowed me to compare the predicted values with the actual data effectively.

• Once we have merged the predicted and actual data into a single table and sorted it accordingly, we proceed to evaluate the accuracy of this algorithm. Our objective is to compare it with the Prophet algorithm and determine its effectiveness. These are the resoults that I got.

This are the results I got:

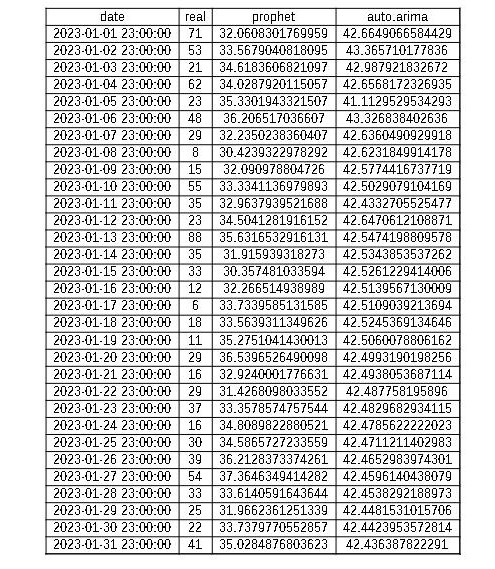
Deduction about the algorithms

• As a small conclusion from my analyzed data, I have noticed that the algorithms do not vary significantly in their predictions. There was not a significant difference between them. However, in the actual data, there were substantial variations. For instance, a value could be 8 on one day and 80 on the next, while both algorithms remained closer to the midpoint and exhibited more stability. They did not exhibit as drastic changes as seen in reality. I observed that with Prophet, the predicted values for PM10 ranged slightly lower, between 30 and 35, while with auto.arima, they were slightly higher, between 40 and 45. In contrast, real-life data showed drastic changes from 8 to 80 or from 20 to 60. The algorithms' predictions tend to average out the values over time since the data is derived from many years of observations. While the predicted values are generally accurate, they do not capture the same level of volatility as observed in reality.

Which algorithm is closest to reality?

Let me provide you with a comparison of the Prophet and auto.arima algorithms using the evaluation metrics I have mentioned: ME, RMSE, MAE, MPE, MAPE, and MASE. I'll go through them one by one and explain which one is better and why. Finally, I'll let you know which algorithm has been more accurate.

• ME (Mean Error):
1. Prophet: -0.925073
2. auto.arima: -9.736052

A value closer to zero indicates better performance. Therefore, Prophet has an ME closer to zero than auto.arima, indicating that Prophet tends to have less bias in its predictions.

• RMSE (Root Mean Squared Error):
1. Prophet: 18.4728
2. auto.arima: 21.25436

RMSE measures the difference between predicted and actual values. A lower value indicates better performance. In this case, Prophet has a lower RMSE than auto.arima, suggesting that Prophet's predictions are generally more accurate.

• MAE (Mean Absolute Error):
1. Prophet: 14.40695
2. auto.arima: 18.45188

MAE also measures the difference between predicted and actual values, but without considering the magnitude of errors. A lower value indicates better performance. In this case, Prophet has a lower MAE than auto.arima, indicating that Prophet's predictions are closer to the actual values, on average.

• MPE (Mean Percentage Error):
1. Prophet: -3.20789
2. auto.arima: -2.2801

MPE measures the average percentage bias of the predictions relative to the actual values. A value closer to zero indicates better performance. Although both values are close to zero, Prophet has an MPE slightly closer to zero than auto.arima, suggesting that Prophet has slightly less bias in its predictions.

• MAPE (Mean Absolute Percentage Error):
1. Prophet: 0.4261506
2. auto.arima: 0.43387

MAPE measures the average percentage error of the predictions relative to the actual values, without considering the magnitude of errors. A lower value indicates better performance. In this case, Prophet has a slightly lower MAPE than auto.arima, suggesting that Prophet's predictions have a lower average percentage error.

• MASE (Mean Absolute Scaled Error):
1. Prophet: 8.855227
2. auto.arima: 84.99589

MASE compares the MAE of the model with the MAE of a naive benchmark model. A lower value indicates better performance. In this case, Prophet has a much lower MASE than auto.arima, indicating that Prophet's predictions are more accurate and significantly outperform the benchmark model.

Considering these metrics, we can conclude that overall, the Prophet algorithm has demonstrated better performance compared to auto.arima. Prophet obtains lower values in several metrics, such as RMSE, MAE, MAPE, and MASE, indicating higher accuracy in its predictions. And the closer to 0 the more accurate is the algorithm. And if we had used the r^2 we needed a closer value to 1.

Comparation of the values of the algorithms vs the real data

• Prophet

• auto.arima

• I have used the libary ggplot and the instruction ggplot(), to realize this plots, and I asked por a "l" plot.

This are the final results:

• If you want to install the pdf here is the link.

Trying another algorithm to predict the future

• I have already done 2 algorithms, but in this project to know which algorithm is better, it is always better to test more in order to have more data to compare. So I have tried to do the algorithm randomForest, that uses thesame library.
• I just wanted to predict the month of January so I needed to set up a time limit to predict, and I have had some issues, because when I tryed seting up the end date, it deleted every value from the table.

• The problem I have had it is that there are some clumns that they don't exist, and that I have to make the table with x and y, for the algorithm to predict it well. I keept having thesame error:

• It keept saying that some values were missing, but in my table in the pm10 values there weren't any missing

Trying SARIMA

• I have also tried doing the algorithm of SARIMA, but it to have it done you need to do an auto.arima, so for me it means the thesame algorithm.
• So, after being unable to make predictions using the Random Forest algorithm due to encountering numerous errors, I found that it was giving me errors stating that there were missing values even though they were present in the table and in the same class as required. This was quite confusing and frustrating.
• I decided to try using two other libraries: Caret and Keras. However, I encountered new errors when attempting to use Keras as it was not detecting the input data (X) and output data (y) necessary for making predictions. Specifically, I received the following error: "Error in quantile.default(y, probs = seq(0, 1, length = groups)): missing values and NaN's not allowed if 'na.rm' is FALSE."
• This error indicates that there were missing values or non-numeric values (NaN) in the output data (y), which is not allowed when 'na.rm' is set to FALSE. In other words, the algorithm expects there to be no missing values or non-numeric values in the output data.
• These errors were quite confusing and hindered my ability to make predictions using these libraries. It seems that there are issues with detecting and handling the data in these libraries, making the prediction process more challenging. I may need to further examine and preprocess my data properly before using these algorithms.
• Because it said that there were some missing values I tried using this funcion "datos_sin_faltantes <- na.omit(datos)", but when I realized it, it completly deleted the whole table.